2022QWB Re find basic

2022强网杯re——find_basic

首先查壳，该程序是一个32位ELF文件

image-20220822163610119

进入main函数，可以看到大量的混淆，每个都是由pushf, pusha, mov, call, pop五个指令为一组进行，与虚拟机混淆十分类似

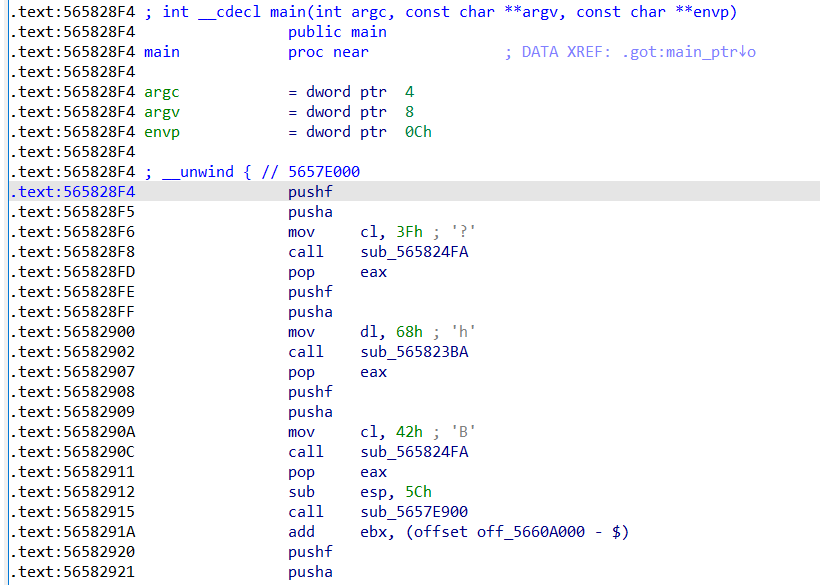
image-20220822163721787

然后在第一个pushf处下断点，直接动态调试（因为就算F5了也没什么用，根本看不懂）

在第一次混淆中每处都F7步入，分析

进入第一个函数

image-20220822164218587

主要会有下面两个函数

image-20220822164536372

继续F7分析，会发现第一个函数的功能就是将一个地址处的值压入EAX寄存器，再加一：

第二个函数

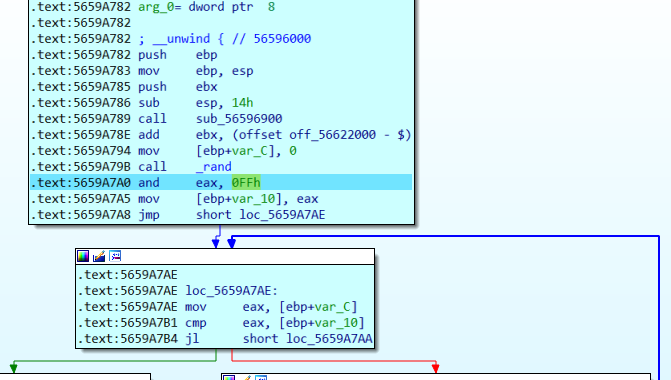
image-20220822164719689

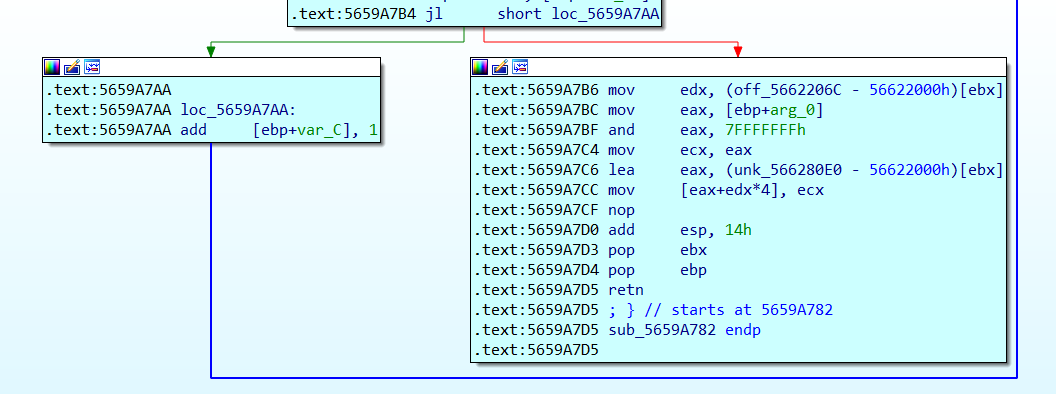
image-20220822164845831

可以看出这里有一个循环，但是每一次左边的操作只有加一，所以直接在右边第一条指令下断点，F9

然后F7直接返回上一个函数

所以这两个函数都是没用的混淆

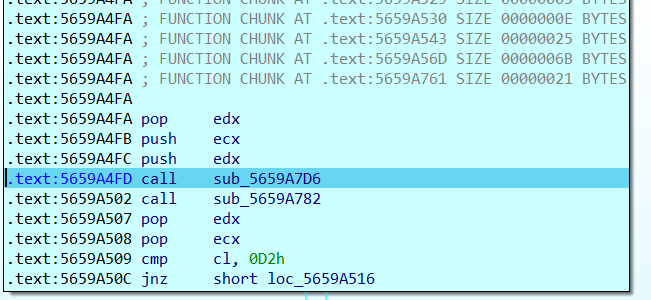
返回之后继续单步步入，发现进行了一些比较后，进行了多次跳转，当c1 == 3Fh时跳转到这里

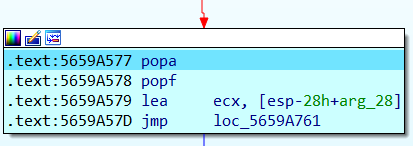
image-20220822165249779

单步步入到这里

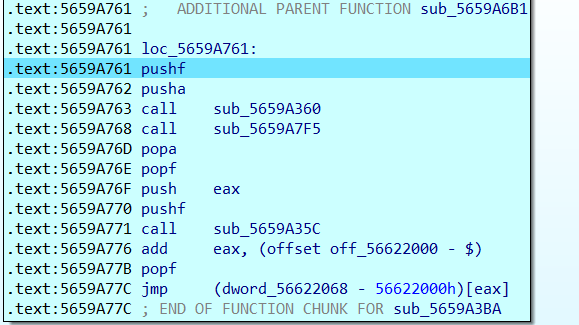
image-20220822165430354

然后步入，发现这些函数都是和前面那些函数形式上差不多的混淆操作，没什么用，只有最后一个函数是前面加一之后的值减一

然后执行jmp跳转

image-20220822165738927

发现程序回到了原点，然后接下来可以继续再跟进下一个函数，发现进行的操作都是同样的，然后接下来不断按下F8步过，

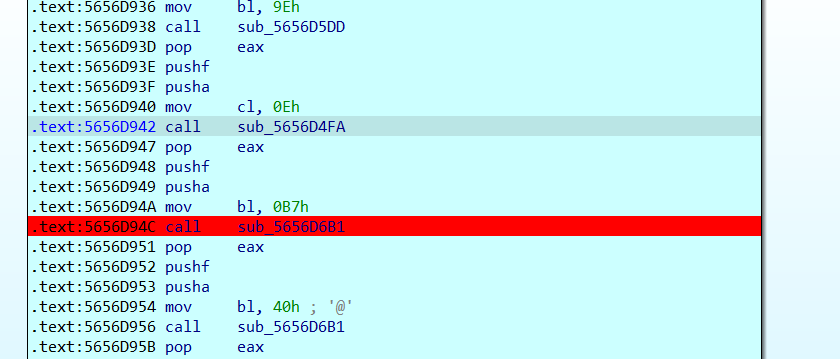
image-20220823105425373

到这里不管怎么按F8都没用了，说明程序要求我们输入了

image-20220822170224743

然后随便输入些什么，主要是方便接下来的跟踪，这里输入123456789，

然后开始F7单步步入，进入到第一个有用代码块

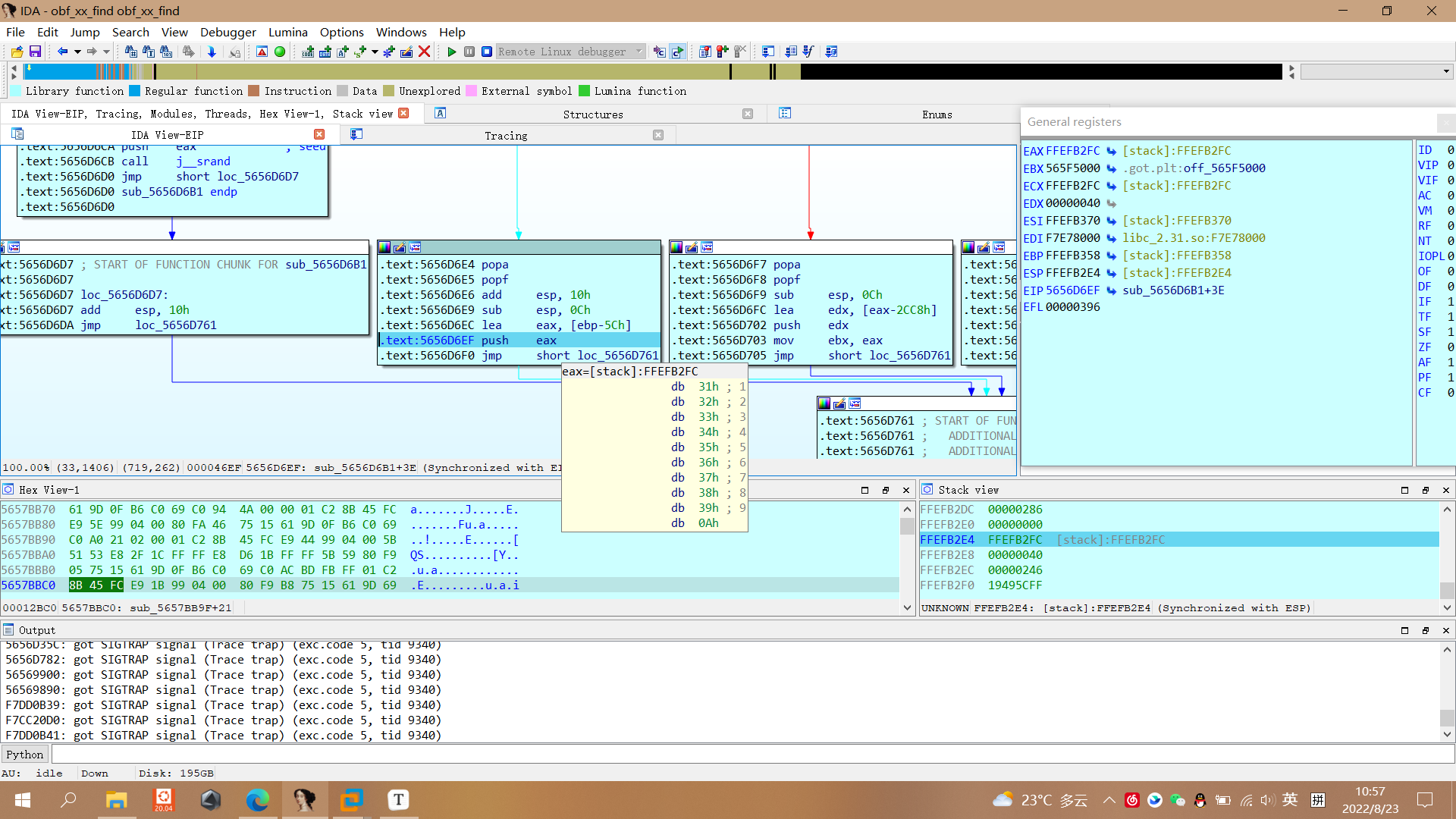
image-20220823105734413

在这里，先将输入的内容保存到了eax中，然后再把它压入堆栈

然后继续步入，到

image-20220823110215865

进入分析这个函数

内层有很多混淆，绝大多数都是没用的函数，但是跳转到有用的指令前都会进行一个cmp指令和jnz指令，成功跳转后的指令就是有用的指令

进入到这里

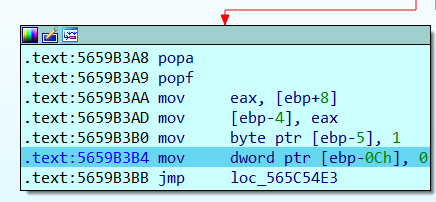
image-20220823110633629

这块的操作就是将我们输入的数据保存

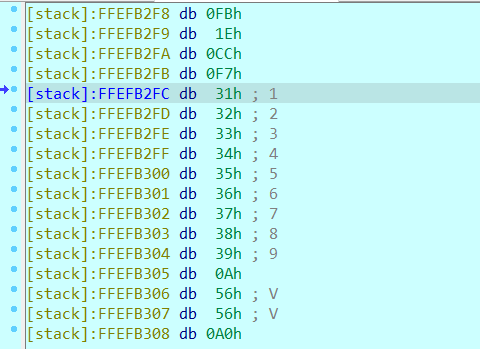
image-20220823110706916

继续步入，到这里，是第一个关键部位

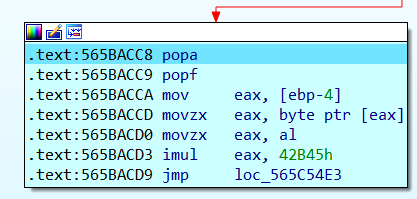
image-20220823110742596

将eax寄存器的内容乘以42B45h，而eax寄存器中保存的内容恰好就是输入的第一个值，在这里也可以看到，就是字符1对应的ASCII码

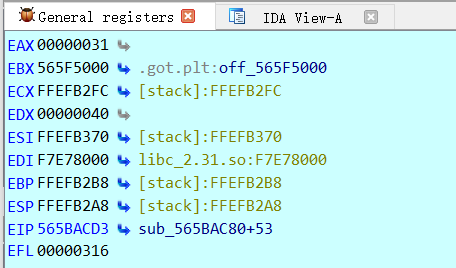
image-20220823110914559

再步入到下一个函数，这里的sub eax, 1A93D7Eh，也相当于是一种比较，如果两个数值相等，执行后ZF会被置为1，如果不相等会被置为0，运行后，ZF为0

至于为什么eax寄存器的值到这一步没有变，可以仔细看前面的push和pop指令，eax寄存器的值在eax被使用之前先被压入栈中，然后在使用完后再出栈，保证了值不会被改变

image-20220823111245821

image-20220823111459859

就可以得到flag[0] * 42B45h == 1A93D7Eh，

然后接下来为了避免复杂的动调，使用IDA的tracing功能

进入这个窗口，发现他什么都没有

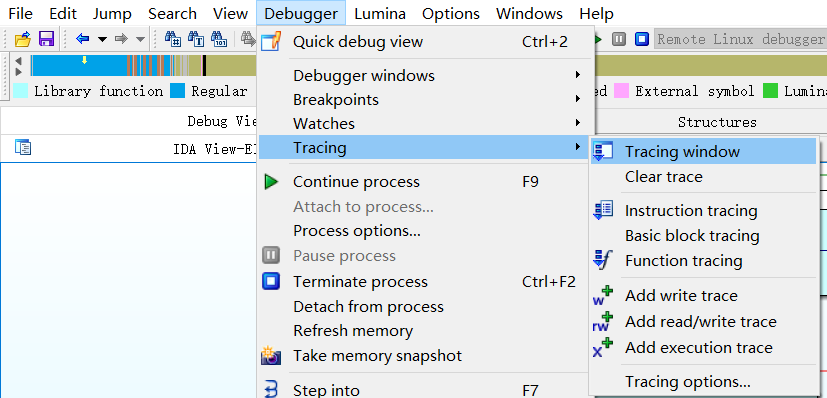
image-20220823111923566

然后打开view——Toolbars——Tracing

image-20220823112006254

然后打开Tracing options

image-20220823112055819

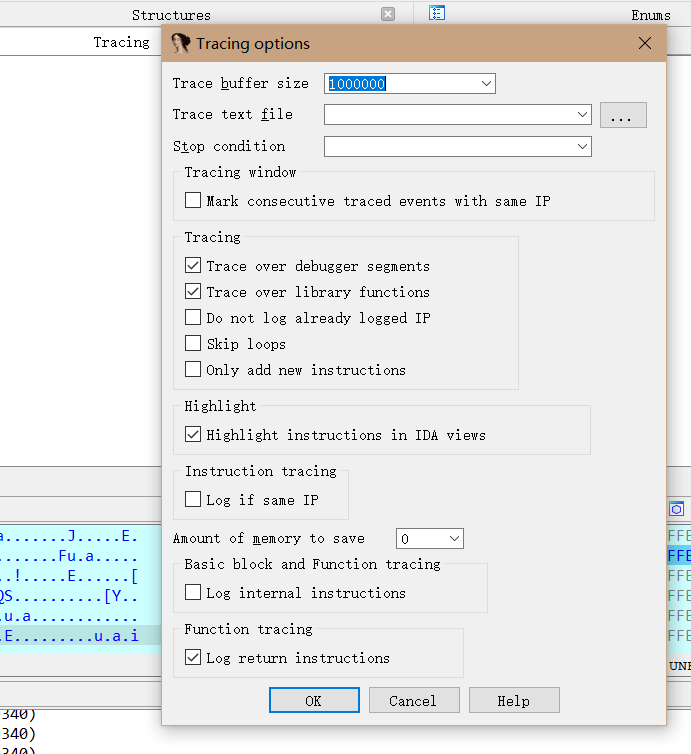
image-20220823112126731

不用修改数据，直接默认，点击OK

然后点亮右上角的这个

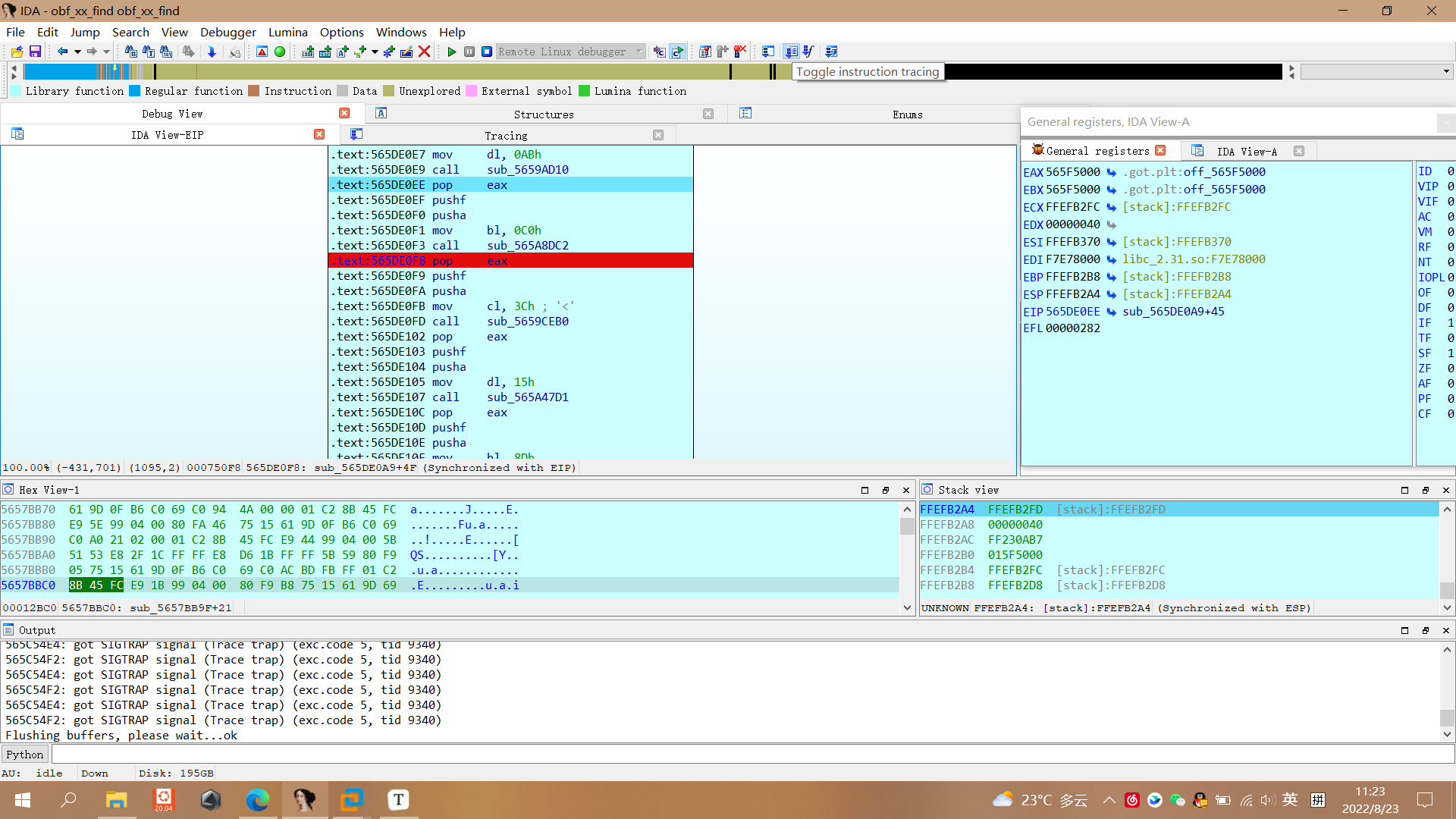
image-20220823112310594

然后下断点，F9运行即可，然后等待一会后，这里就会记录下来刚才所有的指令

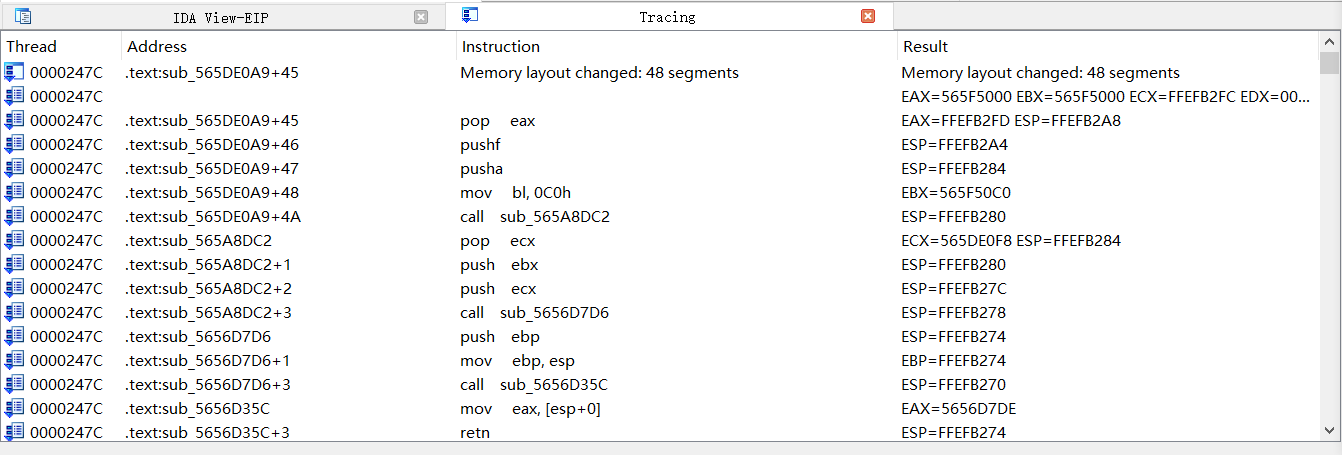
image-20220823112525811

然后将它复制到VScode中，然后直接搜索

image-20220823112930835

因为之前说过，真正的有用代码执行前都会执行cmp和jnz指令，只有cmp的被操作数和在进入混淆前给的字符相同时才会进行

定位到这一块，然后分析

image-20220823113140573

根据之前的特征分析，这一步进行的是flag[1] * 3B10Fh

然后进行相同的方法，下端点，F9（切记要在重新记录前清空Tracing界面）

然后定位到这里

image-20220823113444737

分析出他的指令第一步是 flag[0] * 1E4E0h，然后add指令就是flag[0] * 1E4E0h + flag[1] * 3B10Fh

然后故技重施

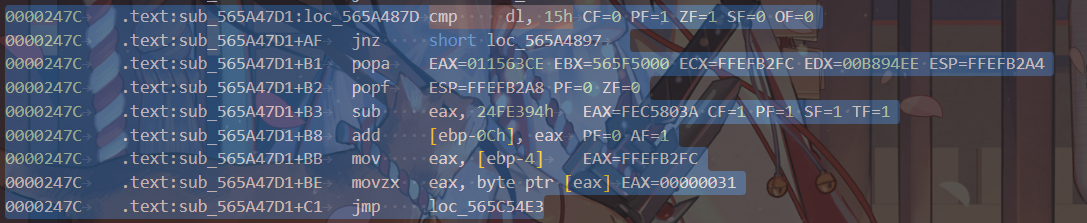
image-20220823113717462

到这里发现，sub eax, 24FE394h，实际上就是flag[0] * 1E4E0h + flag[1] * 3B10Fh == 24FE394h

已经可以想到了，肯定是用到z3的方程组求解，

接下来只需要重复这样的步骤，获取后面的数据，然后再用z3求解

EXP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
from z3 import *

flag = [BitVec('flag[%d]' % i, 8) for i in range(0x1c)]

solver = Solver()

for i in range(0x1c):
    solver.add(flag[i] >= 32)
    solver.add(flag[i] <= 127)

solver.add(flag[0] == ord('f'))
solver.add(flag[1] == ord('l'))
solver.add(flag[2] == ord('a'))
solver.add(flag[3] == ord('g'))
solver.add(flag[4] == ord('{'))
solver.add(flag[-1] == ord('}'))

solver.add(flag[0] * 0x42b45 - 0x1a93d7e == 0)
solver.add(flag[1] * 0x3b10f + flag[0] * 0x1e4e0 - 0x24fe394 == 0)
solver.add(flag[0] * 0x31fc4 + flag[1] * 0xfffdb038 + flag[2] * 0x1390f - 0xbb9e67 == 0)
solver.add(flag[0] * 0x32494 + flag[3] * 0xfffe5a07 + flag[1] * 0xa4e6 + flag[2] * 0x6ba7 - 0x1052718 == 0)
solver.add(flag[1] * 0xfffe0c3f + flag[2] * 0x43e32 + flag[0] * 0x3f49d + flag[3] * 0xc094 + flag[4] * 0xfffb7eff - 0x7fb225 == 0)
solver.add(flag[5] * 0x33e5b + flag[1] * 0x157f8 + flag[4] * 0xd4eb + flag[2] * 0xfffc9ad6 + flag[3] * 0x9c95 + flag[0] * 0xfffd8c2e - 0x6a31d == 0)
solver.add(flag[6] * 0x6d8c + flag[4] * 0xfffedd66 + flag[5] * 0x46fd4 + flag[1] * 0xfffc79bb + flag[3] * 0xfffbe7f5 + flag[2] * 0x14cde + flag[0] * 0xfffc4acd + 0x3083b63 == 0)
solver.add(flag[4] * 0x129fd + flag[7] * 0x2a3cd + flag[5] * 0x52a1 + flag[6] * 0x87de + flag[3] * 0x357c1 + flag[0] * 0xfffbe625 + flag[1] * 0xfffec17b + flag[2] * 0x8039 - 0xd3b6ed == 0)
solver.add(flag[4] * 0xfffe590f + flag[6] * 0xfffc6bb7 + flag[0] * 0x2aec8 + flag[7] * 0xfffd58b1 + flag[3] * 0xfffcf131 + flag[8] * 0xfffc0fae + flag[1] * 0xfffcf46a + flag[2] * 0xfffbbb98 + flag[5] * 0xfffc9913 + 0x7a4d9d3 == 0)
solver.add(flag[6] * 0x3cb6 + flag[5] * 0xfffc5201 + flag[9] * 0xfffdec99 + flag[8] * 0x195a8 + flag[4] * 0xfffbcea6 + flag[7] * 0xfffd4f63 + flag[0] * 0x3852e + flag[3] * 0x36c09 + flag[2] * 0xfffdffc6 + flag[1] * 0xffffbb8f + 0x27b7033 == 0)
solver.add(flag[8] * 0xfffb7a1c + flag[10] * 0xffff35fe + flag[4] * 0xfffe5693 + flag[3] * 0xfffdb9f4 + flag[5] * 0xbd38 + flag[1] * 0x25b89 + flag[2] * 0x3074d + flag[7] * 0xfffe5f6f + flag[9] * 0x1400e + flag[0] * 0xfffcd14c + flag[6] * 0x4036d + 0xa8256 == 0)
solver.add(flag[7] * 0x2da7a + flag[2] * 0xfffbfd56 + flag[9] * 0xffff0011 + flag[0] * 0xfffce077 + flag[3] * 0x34d5d + flag[5] * 0xfffb8def + flag[10] * 0xffff2d4e + flag[4] * 0x237a3 + flag[1] * 0x386e1 + flag[6] * 0xfb89 + flag[8] * 0x2e485 + flag[11] * 0x42574 - 0x24df62a == 0)
solver.add(flag[10] * 0x21c5e + flag[1] * 0x32144 + flag[11] * 0x420e3 + flag[3] * 0x3f6d0 + flag[0] * 0x1a459 + flag[2] * 0xfffc900e + flag[8] * 0x3fd03 + flag[7] * 0x43d16 + flag[5] * 0xfffe4105 + flag[6] * 0xfffd400a + flag[9] * 0xffffc29b + flag[4] * 0x2f9f0 + flag[12] * 0x19432 - 0x6f9b293 == 0)
solver.add(flag[1] * 0xfffca694 + flag[0] * 0xfffce151 + flag[9] * 0x30418 + flag[11] * 0x2f6aa + flag[4] * 0x1b619 + flag[8] * 0x22e4 + flag[7] * 0xfffe1384 + flag[10] * 0xffffa664 + flag[3] * 0x13e07 + flag[2] * 0xfffc46de + flag[5] * 0x79d6 + flag[12] * 0x4372b + flag[13] * 0x3d1d + flag[6] * 0x4d41 - 0x176513c == 0)
solver.add(flag[7] * 0x29b04 + flag[3] * 0xfffd2684 + flag[2] * 0xfffd9a2f + flag[10] * 0xfffd79fc + flag[13] * 0x2594e + flag[12] * 0x41c45 + flag[6] * 0xfffc9c57 + flag[5] * 0xfffc5f95 + flag[11] * 0xfffec65c + flag[14] * 0xffffb642 + flag[1] * 0xfffcb527 + flag[0] * 0x2792e + flag[4] * 0xfffe1bb7 + flag[8] * 0x445a1 + flag[9] * 0xfffd25cc + 0x5338cd6 == 0)
solver.add(flag[14] * 0xfffd399c + flag[3] * 0xffff3edb + flag[11] * 0x26b94 + flag[13] * 0xfffcee81 + flag[4] * 0xfffefe93 + flag[5] * 0xfffcdfa4 + flag[6] * 0xfffe2a42 + flag[0] * 0x10ba4 + flag[10] * 0x38e1d + flag[12] * 0x14c1e + flag[7] * 0xffffce4a + flag[8] * 0xfffd2a4b + flag[9] * 0x41fc + flag[1] * 0xfffedbac + flag[2] * 0xfffeab6a + flag[15] * 0xfffe4e59 + 0x299ff72 == 0)
solver.add(flag[14] * 0xfffdc67b + flag[1] * 0xffffb1fc + flag[12] * 0xffff59be + flag[8] * 0x3684 + flag[5] * 0x202c2 + flag[10] * 0x2e43 + flag[6] * 0xffff3a46 + flag[7] * 0x6a23 + flag[2] * 0xebfb + flag[0] * 0xfffbb78a + flag[15] * 0xd44a + flag[13] * 0x385eb + flag[11] * 0xfffee046 + flag[9] * 0xfffeb282 + flag[4] * 0xfffde639 + flag[3] * 0xfffd6738 + flag[16] * 0xffff1aa3 + 0x4728350 == 0)
solver.add(flag[1] * 0x28c9c + flag[4] * 0xfffdc4ae + flag[3] * 0x278ad + flag[17] * 0x326ca + flag[7] * 0xfffd423d + flag[15] * 0xfffc96fc + flag[10] * 0xfffeeb1a + flag[9] * 0xfffc2ee0 + flag[5] * 0x106be + flag[6] * 0xffff5d67 + flag[8] * 0x27 + flag[11] * 0xfffbc3b6 + flag[12] * 0xfffd163c + flag[13] * 0xfffb9b47 + flag[2] * 0x1e6ed + flag[0] * 0xfffc6c6f + flag[16] * 0x3b32b + flag[14] * 0x2feea + 0x48d1119 == 0)
solver.add(flag[3] * 0xfffc2bb3 + flag[0] * 0xfffce76f + flag[4] * 0xfffca692 + flag[1] * 0xfffdf4bc + flag[14] * 0x192f9 + flag[17] * 0xfffe5a1e + flag[15] * 0xfffed4f3 + flag[7] * 0xffff94f8 + flag[6] * 0xfffc717e + flag[9] * 0xfffed29b + flag[10] * 0xfffd28d9 + flag[8] * 0x218df + flag[2] * 0x28e00 + flag[12] * 0xfffdd0af + flag[13] * 0x25d22 + flag[11] * 0x42ebb + flag[5] * 0xffff1382 + flag[18] * 0x7404 + flag[16] * 0xfffe2dff + 0x60245a5 == 0)
solver.add(flag[5] * 0x21061 + flag[0] * 0xfffbcb01 + flag[19] * 0xffff7442 + flag[3] * 0x24568 + flag[6] * 0x1b201 + flag[13] * 0x2d232 + flag[14] * 0x13777 + flag[7] * 0xfffee013 + flag[8] * 0xfffc7505 + flag[2] * 0x264ed + flag[1] * 0x33b4f + flag[11] * 0x286d8 + flag[17] * 0x33e8b + flag[12] * 0x21529 + flag[16] * 0xfffb7c1a + flag[18] * 0xfffd07a3 + flag[10] * 0xffff8453 + flag[4] * 0x9754 + flag[9] * 0xfffd603d + flag[15] * 0xfffdd85b - 0x254e142 == 0)
solver.add(flag[0] * 0xfffe206e + flag[12] * 0x2f048 + flag[8] * 0xfffc19fa + flag[4] << 6 + flag[7] * 0x370d + flag[13] * 0xfffd9c2f + flag[6] * 0xfffdb413 + flag[20] * 0x30e0a + flag[18] * 0xfffe07f8 + flag[9] * 0xfffedfd5 + flag[10] * 0xfffee6f6 + flag[3] * 0x46247 + flag[1] * 0x2b8ed + flag[16] * 0x2d291 + flag[5] * 0xfffdc54d + flag[15] * 0xfffc5b55 + flag[14] * 0xfffb8061 + flag[11] * 0x43913 + flag[2] * 0xffffe191 + flag[17] * 0xfffd276e + flag[19] * 0xfffe5841 + 0xce53e7 == 0)
solver.add(flag[20] * 0xfffed971 + flag[21] * 0x46741 + flag[18] * 0xfffbac8c + flag[1] * 0xfffeb4e7 + flag[13] * 0x1026b + flag[12] * 0xfffe7d86 + flag[6] * 0xfffd5fec + flag[3] * 0x48ddb + flag[16] * 0xfffc6bc1 + flag[17] * 0x37ece + flag[8] * 0x41105 + flag[2] * 0xfffe6667 + flag[19] * 0xfffe75b2 + flag[4] * 0x61b0 + flag[14] * 0xffffd602 + flag[11] * 0xfffbce29 + flag[0] * 0xffff07d7 + flag[5] * 0x34c8e + flag[15] * 0x32996 + flag[10] * 0x49530 + flag[7] * 0x33822 + flag[9] * 0xfffce161 + 0x42666b == 0)
solver.add(flag[8] * 0xfffe06e8 + flag[12] * 0xfffd0441 + flag[2] * 0x16357 + flag[3] * 0x1d95f + flag[22] * 0xffff89d3 + flag[1] * 0xfffba022 + flag[16] * 0x46180 + flag[4] * 0xffff4240 + flag[5] * 0x199c5 + flag[21] * 0xffff442c + flag[17] * 0xfffc2fac + flag[10] * 0x32600 + flag[19] * 0x1d03a + flag[9] * 0x19435 + flag[15] * 0xfffd1667 + flag[18] * 0x35d1d + flag[0] * 0x96c4 + flag[11] * 0x2fa24 + flag[7] * 0xb20c + flag[6] * 0xebee + flag[20] * 0x428a6 + flag[14] * 0xfffceb8a + flag[13] * 0x22784 - 0x3604a63 == 0)
solver.add(flag[0] * 0x1e3e2 + flag[9] * 0x1cfb9 + flag[6] * 0xc3f7 + flag[10] * 0x94cd + flag[22] * 0xfffc7fd0 + flag[2] * 0x21165 + flag[23] * 0xfffcfb41 + flag[14] * 0xffff819d + flag[5] * 0xfffbeb76 + flag[1] * 0x16751 + flag[19] * 0xe1a + flag[17] * 0x238a0 + flag[12] * 0x28f99 + flag[8] * 0x45bc + flag[20] * 0xffffcb18 + flag[15] * 0x32d58 + flag[11] * 0xffffe4bc + flag[16] * 0xfffeea95 + flag[13] * 0x44f3a + flag[18] * 0xb047 + flag[7] * 0xfffcfc36 + flag[21] * 0x1719 + flag[4] * 0x1b011 + flag[3] * 0xfffea265 - 0x2918269 == 0)
solver.add(flag[15] * 0xfffbf307 + flag[8] * 0xffff2847 + flag[6] * 0xfffcfd31 + flag[2] * 0x40f96 + flag[22] * 0x2b265 + flag[5] * 0xfffc7802 + flag[3] * 0x1b103 + flag[4] * 0x42452 + flag[14] * 0x3c5d + flag[1] * 0x15b55 + flag[9] * 0xfffeb722 + flag[13] * 0x1d9a9 + flag[23] * 0x28df + flag[12] * 0xfffc89eb + flag[10] * 0xfffe1221 + flag[7] * 0x4462a + flag[19] * 0x23353 + flag[21] * 0x3c514 + flag[0] * 0x316a4 + flag[11] * 0x176e1 + flag[20] * 0xcf0e + flag[18] * 0x46b55 + flag[24] * 0xffffbcc1 + flag[17] * 0xf2a7 + flag[16] * 0x1d33c - 0x5df35b6 == 0)
solver.add(flag[3] * 0xfffbf624 + flag[22] * 0xfffec87a + flag[2] * 0x19aaa + flag[23] * 0x5f14 + flag[20] * 0xfffcfc43 + flag[16] * 0xfffbe879 + flag[15] * 0xfffdfc92 + flag[14] * 0xffffc258 + flag[0] * 0xfffd02fd + flag[5] * 0x12560 + flag[13] * 0xae46 + flag[7] * 0xfffeb6f5 + flag[12] * 0x30c11 + flag[17] * 0xfffcb4ae + flag[24] * 0x2a00a + flag[6] * 0xfffc76de + flag[21] * 0x4162 + flag[10] * 0xfffe95b2 + flag[25] * 0xfffe60e7 + flag[19] * 0xffff908d + flag[4] * 0xfffb7f42 + flag[11] * 0x1c31 + flag[1] * 0xffff900c + flag[8] * 0x2ad6e + flag[9] * 0xfffd7c6d + flag[18] * 0xc499 + 0x83646cd == 0)
solver.add(flag[12] * 0x26b02 + flag[3] * 0xfffb92e5 + flag[17] * 0x30dd1 + flag[18] * 0xfffe4c7b + flag[0] * 0xffff0433 + flag[1] * 0x276b1 + flag[9] * 0xfffc241e + flag[5] * 0xfffe3fdc + flag[8] * 0xfffee787 + flag[10] * 0x230c + flag[21] * 0xfffd53f8 + flag[4] * 0xfffc108c + flag[14] * 0xffffbac1 + flag[26] * 0xffff0bdb + flag[15] * 0xfffbc5e2 + flag[19] * 0xa1f6 + flag[16] * 0x1e758 + flag[22] * 0x1725f + flag[23] * 0x3387e + flag[20] * 0x87b + flag[2] * 0xfffd8475 + flag[13] * 0x3776a + flag[24] * 0xffff4515 + flag[11] * 0x1a454 + flag[6] * 0xfffbf3a1 + flag[25] * 0x25174 + flag[7] * 0xfffbccc2 + 0x52dfb3f == 0)
solver.add(flag[25] * 0x2f139 + flag[20] * 0x21b53 + flag[15] * 0x2ad74 + flag[9] * 0xfffba19b + flag[16] * 0x1ac4e + flag[27] * 0x2208e + flag[13] * 0xfffdd738 + flag[11] * 0xfffdfb9f + flag[8] * 0xfffe4b65 + flag[5] * 0x10937 + flag[10] * 0xfffbfdf3 + flag[12] * 0x3cc1a + flag[23] * 0xfffe93ee + flag[2] * 0xfffe3b8a + flag[14] * 0xfffe792c + flag[6] * 0x3e9ff + flag[21] * 0x128e6 + flag[3] * 0x574b + flag[24] * 0x16707 + flag[19] * 0x3fe4c + flag[17] * 0xfffed658 + flag[7] * 0x3cc8c + flag[22] * 0x458b4 + flag[1] * 0xfffd74d0 + flag[18] * 0x22e02 + flag[4] * 0xffff098d + flag[0] * 0x30b99 + flag[26] * 0xfffba5e9 - 0x38186f4 == 0)

flag_str = ''

if solver.check() == sat:
    m = solver.model()
    for i in range(0x1c):
        flag_str += chr(m[flag[i]].as_long())

print(flag_str)

#flag{U_90t_th3_8451c_53cre7}

这种单步调试的方法很慢而且容易出错，后面看wp时看到了一个解决方法，直接写python脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
from idaapi import *
from ida_ua import *
from keystone import *
from capstone import *
ks = Ks(KS_ARCH_X86, KS_MODE_32)
cs = Cs(CS_ARCH_X86, CS_MODE_32)
insn = insn_t()
b = bytearray()

def dis(bytecode, address):
    for i in cs.disasm(bytecode, address):
        res = i.mnemonic + ' ' + i.op_str
        return res

def get_valid_code(addr):
    global b
    func_ea = addr
    while True:
        s = GetDisasm(func_ea) # 获取当前指令
        if s == 'pushf': # 获取dispatcher结果
            # pushf -> pusha -> mov -> call -> pop
            l = decode_insn(insn, func_ea)
            func_ea += l # jmp pushf
            l = decode_insn(insn, func_ea)
            func_ea += l # jmp pusha
            # mov
            opcode = get_operand_value(func_ea, 1)
            reg = get_operand_value(func_ea, 0)
            l = decode_insn(insn, func_ea)
            func_ea += l # jmp mov
            call_func_ea = get_operand_value(func_ea, 0)
            l = decode_insn(insn, func_ea)
            func_ea += l # jmp call
            l = decode_insn(insn, func_ea)
            func_ea += l # jmp pop
            #print(hex(call_func_ea))
            while True: # 找到对应分支
               s = GetDisasm(call_func_ea)
               if s[:3] == 'cmp':
                   cmp_opcode = get_operand_value(call_func_ea, 1)
                   cmp_reg = get_operand_value(call_func_ea, 0)
                   if cmp_opcode == opcode and cmp_reg == reg: # find!
                       l = decode_insn(insn, call_func_ea)
                       call_func_ea += l # jmp cmp
                       break
               length = decode_insn(insn, call_func_ea) # 获取指令长度
               call_func_ea += length
            # cmp -> jnz -> popa -> popf -> valid code
            #print(hex(opcode))
            l = decode_insn(insn, call_func_ea)
            call_func_ea += l # jmp jnz
            l = decode_insn(insn, call_func_ea)
            call_func_ea += l # jmp popa
            l = decode_insn(insn, call_func_ea)
            call_func_ea += l # jmp popf
            # jump to valid code
            s = GetDisasm(call_func_ea)
            if s == 'pushf':
                # retn
                b += b'\xC3'
                continue
            while True:
                s = GetDisasm(call_func_ea)
                #print(s)
                if s[:3] == 'jmp':
                   # retn
                   break
                # get valid code
                length = decode_insn(insn, call_func_ea) # 获取指令长度
                #print(length,hex(call_func_ea))
                disas = dis(get_bytes(call_func_ea, length), call_func_ea)
                b += bytes(ks.asm(disas, call_func_ea)[0])
                call_func_ea += length
        else: # 正常代码
            length = decode_insn(insn, func_ea) # 获取指令长度
            disas = dis(get_bytes(func_ea, length), func_ea)
            b += bytes(ks.asm(disas, func_ea)[0])
            func_ea += length
            if s == 'retn':
                break
valic_code_addr = 0x8C100
get_valid_code(0x48F4)
get_valid_code(0x48C8)
get_valid_code(0x3FBF)
get_valid_code(0x3F1B)
get_valid_code(0x4148)
get_valid_code(0x750A9)
get_valid_code(0x33EC)
patch_bytes(valic_code_addr, bytes(b))
print('done!')

具体可以参考【CTF&WP】2022强网杯Reverse——find_basic_哔哩哔哩_bilibili

2022–第六届“强网杯”全国网络安全挑战赛—WriteUp - Bit’s Blog (xl-bit.cn)

reverse
#强网杯
2022QWB Re find basic
http://example.com/2022/10/09/2022QWB-Re-find-basic/
Author
Eutop1a
Posted on
October 9, 2022
Licensed under